[항해 플러스 코육대] 회고 - 애자일하게 테트리스 만들기

플레이 해보기 : https://wooseob.github.io/ 조작키 좌/우 방향키 : 좌/우로 이동 위쪽 방향키 : 테트로미노 회전 아래쪽 방향키 : 한칸 더 빠르게 내려가기 스페이스 바 : 테트로미노 바닥까지 바로 내려보내기 Github Repository : https://github.com/WooSeob/wooseob.github.io/tree/kyd-feature/base 1. 기능 구현 설명 여러가지 기능의 나열을 하기보단 개발 과정이 뒤돌아보니 애자일이었다는 생각이 들었다. (테스트 코드를 통한 자동화된 테스트는 아니고 직접 로컬에서 확인했으나 시간은 많이 안걸렸다^^) 이런 관점에서 기능을 소개하고자 한다. 1) 블럭부터 찍어보기 먼저, 테트리스를 만들기로 했는데 테트리스를 즐겨하지 않..

WSL2 [코드 4294967295로 프로세스 종료됨] 오류 해결 BIOS 가상화 해결

평소에 개발환경을 WSL2로 세팅해놓고 개발을 하곤 했는데, 어느날 갑자기 가상 머신 플랫폼 Windows 기능을 사용하도록 설정하고 BIOS에서 가상화를 사용 하도록 설정되어 있는지 확인하세요. 자세한 내용은 https://aka.ms/wsl2-install을 참조하세요. [코드 4294967295로 프로세스 종료됨] 이런 로그가 뜨며 WSL이 작동이 안되더라 에러 메시지 그대로 구글링 해봤지만 1페이지에 올라온 거의 모든 글들이 같은내용.. 해결은 되지 않고 겨우 github issue를 하나 찾았고 거기서 해결 방법을 얻었다. Spacedesk 문제일거라곤 상상도 못했고, 한글로 검색했을땐 감도 못잡았다. 역시 구글링은 영어로.. 허무하고 열받아서 한글로 검색해서 나같이 삽질하지 마시라고 내가 정리..

heroku 환경변수

[Java] 람다식(Lambda Expressions)

1. 익명 클래스 자바에는 익명클래스를 통해서 재사용 되지도 않을 클래스가 계속 쌓이는것을 막을 수 있다. 대표적으로 쓰레드를 생성할때 아래와 같은 방법을 주로 사용한다. Thread t = new Thread(new Runnable() { @Override public void run() { while (true) { System.out.println(Thread.currentThread().getName() + " : hello world"); } } }); 하지만 자바스크립트에 익숙한 사람이라면 위의 코드마저도 자바스크립트에서 콜백을 사용하는 방식과 비교해 보면 불필요한 코드가 굉장히 많다고 느껴질것이다. 2. 함수적 인터페이스 Runnable 인터페이스를 까보면 아래와 같다 @FunctionalI..

Angular 표현식

리액트는 비교적 편하게 입문한 기억이 있는데 Angular는 독자적인 것들이 너무 많아서 정신나갈것같다^^ 정리해보자. (click)=" EXPRESSION " 해당 태그의 클릭 이벤트를 등록한다. *ngIf="BOOLEAN" 불리언식이 true면 해당 태그를 표시하고 false면 표시하지 않는다 (ngSubmit)="CALLBACK()" form 태그의 action을 대체하는 용도. 컴포넌트.ts에 들어있는 함수들이 콜백의 범위인것 같다. [(ngModel)]="VARIABLE" 입력 폼에서 받은 값을 해당 변수에 바인딩한다 ngModule을 임포트 해줘야 한다고한다 *ngFor="EXPRESSION(for문)" 해당 태그에 대해서 for문을 수행할 수 있도록 해준다. [ngSwitch]="VARIAB..

선택 알고리즘

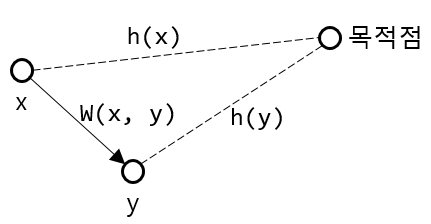
n개의 원소로 이루어진 집합에서 최소/최대 원소를 찾기 위해서는 선형시간 O(n)이 필요하다 적어도 모든원소를 한번씩은 봐야하는 것이다. 그렇다면 최소(혹은 최대) 원소가 아닌 2번째로 작은(혹은 큰) 원소를 찾기 위해서는 최소(최대)원소를 구하는 기본 과정에 2번째로 작은 원소를 저장하고 이를 갱신하는 과정을 추가 하면 된다. 위 과정은 최소/최대 원소를 구하는 과정보다 시간이 더 걸리긴 하지만 마찬가지로 선형시간내에 구할 수 있다. 하지만 n개의 원소로 이루어진 집합에서 중앙값을 구한다고 하면 위 과정에서 n/2번째 원소까지를 저장하며 갱신해야 하므로 이런 경우에는 O(n^2)의 시간이 걸리게 된다. 이런 경우에는 위와같은 방법을 사용하기보단 O(nlogn)시간이 소요되는 정렬 알고리즘을 통해 배열을..

상태 공간 트리 (State-Space Tree)

문제 해결 과정의 중간 상태를 각각 한 노드로 나타낸 트리를 상태 공간 트리(State-Space Tree)라고 한다. 이러한 상태 공간 트리를 탐색하는 방식들에 대해서 이야기 하고자 한다. 1. 백트래킹 (Backtracking) 백트래킹은 주어진 상태 공간 트리를 트리의 루트에서 시작해서 DFS 방식으로 탐색을 해 나가는 것이다. 탐색을 하다가 더 갈 수 없으면 왔던 길을 되돌아가 다른 길을 찾는다고 해서 이런 이름이 붙었다고 한다. 대표적으로 미로 찾기 문제와 색칠 문제가 있다. 미로 찾기 문제 만약 우리가 미로에 갇히게 되면 어떻게 탈출해야할까? 갈 수 있는곳을 일단 가보고, 막다른길이 있다면 왔던길을 되돌아와 가보지 않은 길을 선택하는 행동을 출구가 나올때 까지 반복할 것이다. 미로 -> 상태 ..

동적 프로그래밍 (Dynamic Programming)

동적 프로그래밍은 재귀적으로 구현한 알고리즘에서 중복 호출이 일어나 심각한 비효율이 발생할 때 이를 해결하는 방법이다 예를들어 피보나치 수를 아래와 같이 정의할 때 f(n) = f(n-1) + f(n-2) f(1) = f(2) = 1 * n은 자연수 n번째 피보나치 수 f(n)(n>2)은 피보나치 수 f(n-1)와 피보나치 수 f(n-2) 를 포함한다. 이와같이 큰 문제의 해답에 그보다 작은 문제의 해답이 포함되어 있을 때 최적 부분 구조(Optimal Substructure)를 가졌다고 하고, 아래와 같은 재귀호출로 자연스럽게 구현할 수 있다. def fibo(n) if n==1 or n==2: return 1 else: return fibo(n-1) + fibo(n-2) 중복호출로 인한 비효율이 있는..